We have the expression:
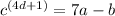
We can apply logarithm to both sides. We would use it in order to get "4d+1". Then, we would apply logarithm with base c. This is beacuse of the definition of logarithm:
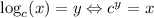
If we apply this to our expression, we get:
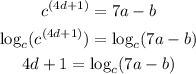
If we rearrange both sides, we get the expression in Option B (we have to switch the sides):
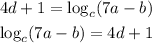
Answer: Option B