As a general rule, we know that the area of a dilated figure is the area of the original figure multiplied by the square of the scale factor. We can see this in the following formula:
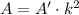
where A is the area of the original figure, A' is the area of the dilated figure and k is the scale factor.
In this case, we have that the area of the dilated figure (trapezoid A'B'C') is 12 square units, and the scale factor is k = 2/3. Then, using the equation we get the following:
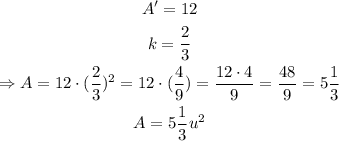
therefore, the area of trapezoid ABCD is 5 1/3 square units