We have a right triangle and we have to write some of the trigonometric ratios.
A trigonometric ratio relates a trigonometric function of an angle of the tiangle with a quotient of two of the sides of the triangle.
The basic trigonometric ratios are:
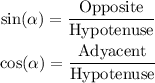
We can also write the trigonometric ratio for the tangent:
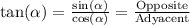
Now, we can write sin(x):
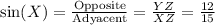
The opposite side to X is YZ and the hypotenuse is XZ, so sin(X) = YZ/XZ = 12/15.
In the same way, we can calculate cos(x):
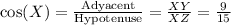
The tan(x) can be calculated as:
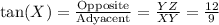
For Z, the opposite and adyacent angles are different than for X, so we can write:
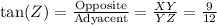
Answer:
sin(X) = 12/15
cos(X) = 9/15
tan(X) = 12/9
tan(Z) = 9/12