Question

PLEASE HELP ME WITH THE QUESTION IN THE PIC BELOW

Answer 1

Let's calculate the distance between F and G:

F=(-4,-2)

G=(2,-2)

`d=\sqrt[]{(2-(-4))^2+(-2-(-2))^2}=\sqrt[]{36}=6`

The distance between M and P is half the distance between F and G, so:

`(d)/(2)=3`

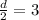
The coordinates of P are:

P=(2,-8)

and

M=(x,-8)

So:

`\begin{gathered} 3=\sqrt[]{(x-2)^2+\mleft(-8-\mleft(-8\mright)\mright)^2} \\ 3=x-2 \\ \text{solving for x:} \\ 3+2=x \\ 5=x \\ x=\pm5 \\ \end{gathered}`

Since M is in the 3rd quadrant:

M= (-5,-8)

----------------------------------------------

Let:

(x1,y1)=(-2,1)

(x2,y2)=(-5,4)

`\begin{gathered} d=\sqrt[]{(x2-x1)^2+(y2-y1)^2} \\ d=\sqrt[]{(-5-(-2))^2+(4-1)^2} \\ d=\sqrt[]{9+9}=\sqrt[]{18} \end{gathered}`