Question

Instructions: Find the surface area of each figure. Round your answers to the nearest tenth, if necessary. 8 cm. 5 cm. 9 cm. 4 cm. 10 cm. Surface Area: cm2

Answer 1

Step 1

State the number of shapes in the figure

The shape is made up of

2 triangles

and

3 rectangles

Step 2

State an expression for the area of a triangle and find the area of the triangle

`\text{The area of a triangle ( A}_1)\text{ = }(1)/(2)* base\text{ }* height`

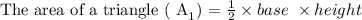
Where the base = 10cm

height = 4cm

The area of the triangle after substitution is

`\begin{gathered} A_1=(1)/(2)*10*4 \\ A_1=20cm^2 \end{gathered}`

Since there are two triangles total area of the triangles = 2 x 20 = 40cm²

Step 3

State the expression for the area of a rectangle

`\text{Area of a rectangle = Length }* width_{}`

Where

For rectangle 1

length = 8cm

width = 9cm

Area of rectangle 1 after substitution = 8 x 9 = 72cm²

For rectangle 2

length = 10cm

width= 9cm

Area of rectangle 2 after substitution = 9 x 10 = 90cm²

For rectangle 3

length = 5cm

wiidth = 9cm

Area of rectangle 3 after substitution = 9 x 5 = 45cm²

Step 4

Find the total area of the shape

`\text{Total surface area of the shape = 45 +90 +}72+40=247cm^2`

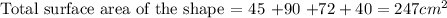
Therefore the surface area of the shape = 247cm²