The Solution:
Given the figure below:
Solving for arc JK:
By angle subtends at the center of a circle is twice that subtends on the circumference, we have that:
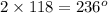
Subtracting 236 from 360, we get
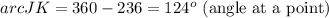
So, the correct answer for question 7 is [option 4]
To answer Question 8:
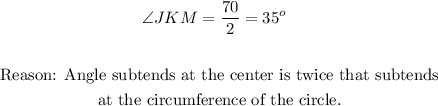
Similarly,
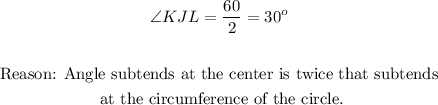
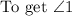
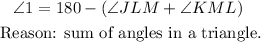
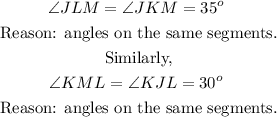
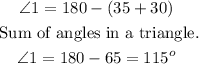
Therefore, the correct answer to Question 8 is 115 degrees.