Question

(G.12, 1 point) Which point lies on the circle represented by the equation (x-4)2 + (y - 2)2 = 72? O A. (-1,4) B. (8,3) O C. (9,0) O D. (-2, 2)

Answer 1

`(x-4)^2+(y-2)^2=7^2`

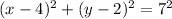
To know if a point lies on a circle you use the (x,y) of each point in the equation and prove it that correspond to a mathematical congruence.

A. (- 1 , 4)

`\begin{gathered} (-1-4)^2+(4-2)^2=7^2 \\ -5^2+2^2=49 \\ 25+4=49 \\ 29=49 \end{gathered}`

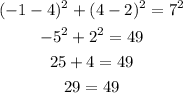
As 29 is not equal to 49, this point doesn't lie in the circle

B. ( 8 , 3)

`\begin{gathered} (8-4)^2+(3-2)^2=7^2 \\ 4^2+1^2=49 \\ 16+1=49 \\ 17=49 \end{gathered}`

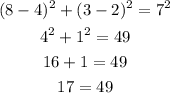
As 17 is not equal to 49, this point doesn't lie in the circle

C. (9 , 0)

`\begin{gathered} (9-4)^2+(0-2)^2=7^2 \\ 5^2+(-2)^2=49 \\ 25+4=49 \\ 29=49 \end{gathered}`

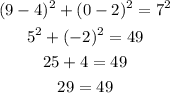
As 29 is not equal to 49, this point doesn't lie in the circle

D. (-2 , 2)

`\begin{gathered} (-2-4)^2+(2-2)^2=7^2 \\ -6^2+0^2=49 \\ 36=49 \end{gathered}`

As 36 is not equal to 49, this point doesn't lie in the circle

None of the points lies on the circle.

The next graph represents the circle and the 4 given points: