Given:
The speed is 64 feet per second.
The height of the high cliff is 80 feet.
The function is
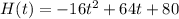
a)
We need to find the maximum value of t in the given function to find a time when the rock reaches its maximum height.
Differentiate the given equation, we get
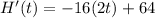
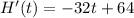
Set H'(t)=0 and solve for t.
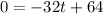
Adding 32t on both sides, we get
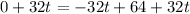
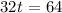
Dividing both sides by 32, we get
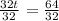
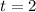
Hence the rock reaches its maximum height after 2 seconds.
b)
Substitute t=2 in the given equation to find the maximum height of the rock.
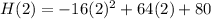
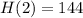
Hence the maximum height obtained by the rock is 144 feet above sea level.
c)
Substitute H(t)=0 in the given function to find the time when the rock hit the ocean.
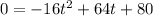
Dividing both sides by (-16), we get
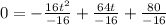
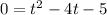


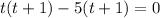
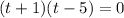
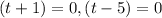

Omitting the negative value, we get t= 5 seconds.
Hence the rock hits the ocean after 5 seconds.