Question

• An ice cube is slowly melting, losing 3cm^3 of water each hour. If it is always a perfect cube, (V=s^3), what is the rate of change of its side length when it has 8 cm^3 of ice left?

Answer 1

Given:

The volume is decreasing at the rate of 3 cm^3 per hour.

The volume of the left ice is 8 cm^3.

Aim:

We need to find the rate of change of the side of the cube.

Step-by-step explanation:

Let the length of the cube is denoted as s.

Consider the volume of the cube.

`V=s^3`

Since the volume is decreasing at the rate of 3 cm^3 per hour. we can write,

`(dV)/(dt)=-3cm^3\/h`

where t represents time and the negative sign represents decreasing.

Differentiate the volume with respect to s.

`(dV)/(ds)=(d)/(ds)(s^3)=3s^2`

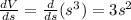
To find the rate of change of the side length, we use the chain rule.

`(dV)/(dt)=(dV)/(ds)(ds)/(dt)`

`\text{ Substitute }(dV)/(dt)=-3\text{ and }(dV)/(ds)=3s^2\text{ in the equation.}`

`-3=(ds)/(dt)(3s^2)`

`-(3)/(3s^2)=(ds)/(dt)`

`-(1)/(s^2)=(ds)/(dt)`

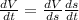
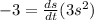
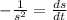
Since the left ice is 8 cm ^3.

`V=(s)^3=8`

`s^3=2^3`
`s=2cm`

`Substitute\text{ s =2 in the equation}-(1)/(s^2)=(ds)/(dt).`

`-(1)/(2^2)=(ds)/(dt).`

`(ds)/(dt)=-(1)/(4)`

`(ds)/(dt)=-0.25cm\text{ per hour}`

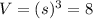
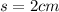
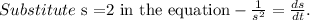
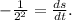
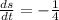
Verification:

Let s =2 cm, then the volume is 8cm^3.

Let s =1.75cm, the volume is