Question

Determine the amount of an investment if $100 is invested at an interest rate of 5.5% compounded semi-annually for 6 years.

Answer 1

We have an investment that is compounded semi-anually.

The equation for the future value of an compounded interest investment is:

`FV=PV(1+(r)/(m))^(n\cdot m)`

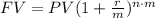
where:

FV is the future value.

PV is the present or initial value of the investment (PV=100).

r is the annual nominal interest rate (r=5.5%=0.055).

m is the number of capitalization subperiods in the year. In this case, as it is semiannually, m=12/6=2.

n is the number of yearly periods that the investment last (n=6 years).

Then, we can replace the variables with the values and calculate:

`\begin{gathered} FV=100\cdot(1+(0.055)/(2))^(2\cdot6) \\ FV=100\cdot(1+0.0275)^(12) \\ FV=100\cdot1.0275^(12) \\ FV\approx100\cdot1.3848 \\ FV\approx138.48 \end{gathered}`

Answer: the value of the investment after 6 years is $138.48.