Answer:
![y=\left[x-\left(-2\right)\right]^2+\left(-9\right)](https://img.qammunity.org/2023/formulas/mathematics/college/lvjhw0pjntjvclkfva01jyn0vyfvhnzgij.png)
Step-by-step explanation:
Given the quadratic equation in standard form:
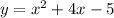
1. Transpose the c-value to the left side of the equation.
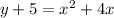
2. Complete the square of the expression on the right side of the equation to get a perfect square trinomial. Add the resulting term to both sides.
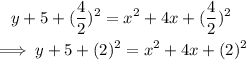
3. Add the numbers on the left and factor the trinomial on the right.
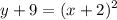
4. Transpose the number across to the right side to get the equation into the vertex form, y=a(x-h)²+k.
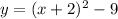
5. Make sure the addition and subtraction signs are correct to give the proper vertex form.
![y=\left[x-\left(-2\right)\right]^2+\left(-9\right)](https://img.qammunity.org/2023/formulas/mathematics/college/lvjhw0pjntjvclkfva01jyn0vyfvhnzgij.png)
The vertex form of the given quadratic equation is:
![y=\left[x-\left(-2\right)\right]^2+\left(-9\right)](https://img.qammunity.org/2023/formulas/mathematics/college/lvjhw0pjntjvclkfva01jyn0vyfvhnzgij.png)