Question

Given f(x)=2x-1 and g(x) =x^2 -2A) f(5)B) f(g(3))C) f(a+1) - f(a)D) g(2f(-1))E) g(x+h) -g(x)/h

Answer 1

2x + h

Step-by-step explanation:

Given the following functions

f(x) = 2x - 1

g(x) = x^2 - 2

We are to simplify the expressionn:

`(g(x+h)-g(x))/(h)`

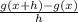
Substitute the given functions into the expression and simplify

`\begin{gathered} (\lbrack(x+h)^2-2\rbrack-(x^2-2))/(h) \\ \frac{\lbrack\cancel{x^2}^{}+2xh+h^2-\cancel{2}-\cancel{x^2}^{}+\cancel{2}}{h} \\ (2xh+h^2)/(h) \end{gathered}`

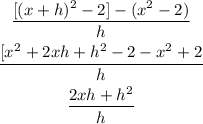
Factor out "h" from the numerator to have:

`\begin{gathered} \frac{\cancel{h}(2x+h)}{\cancel{h}} \\ 2x+h \end{gathered}`

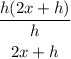
Hence the simplified form of the expression is 2x + h