Question

The remains of an ancient ball court include a rectangular playing alley with a perimeter of about 18m. The length of the alley is two times the width. Find the length and the width of the playing alley.The width is ? m and the length is ? m.

Answer 1

Given:

Perimeter = 18 m

The formula for the perimeter of a rectangle is:

`P=2l+2w`

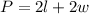
Where:

l = lenght

w = width

In this case, we have that:

l = 2w

Therefore, we substitute the values in the formula:

`\begin{gathered} P=2l+2w \\ 18=2(2w)+2w \end{gathered}`

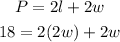
And solve for w:

`\begin{gathered} 18=4w+2w \\ 18=6w \\ (18)/(6)=(6w)/(6) \\ w=3 \end{gathered}`

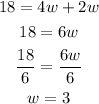
For the length:

`l=2w=2(3)=6`

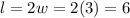
Answer:

The width is 3 m

The length is 6 m