1 Answer

MatthewG · Answer 1 · 2023-07-02T20:51:40+0000

Given that the frequency of the wave is, f = 450 Hz

and the length of the guitar string is, L = 80 cm = 0.8 m

We have to find the speed of the wave, v.

As the frequency is the fundamental frequency, so it will be the first harmonic.

The formula to find the wavelength is

$\lambda=2L$

Substituting the values, we get

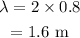
$\begin{gathered} \lambda=2*0.8 \\ =1.6\text{ m} \end{gathered}$

The formula to find the speed of the traveling wave is

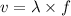
$v=\lambda* f$

Substituting the values, we get

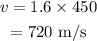
$\begin{gathered} v=1.6*450 \\ =720\text{ m/s} \end{gathered}$

Thus, the speed of the traveling wave is 720 m/s

Please log in or register to add a comment.