Ratios
Note A has a frequency of
fa=1,760 Hz
Note D has a period of 1,175 hertz
(the previous data should be frequency, not period)
We are required to find the ratio of A to D. Let's call it r:
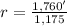
Dividing: r = 1.4978. Rounding to two decimal places:
r = 1.50
Now to express the answer in integer ratio form, we need to simplify the fraction.
First, we divide by 5 up and down:
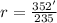
There are no more common divisors for both numbers, thus the integer ratio form is r = 352/235