Given:
Sample Size (n) = 425
No. of Success = 121
Find: estimate the proportion of the population
Solution:
Let's calculate first the success proportion in the sample by dividing no. of success over the total number of people then multiply it by 100.
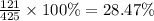
Our sample proportion p = 28.47%.
Then, for the margin of error, the formula is:
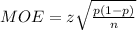
where z = critical value, p = sample proportion, and n = sample size.
For our z-value, since we are using a 95% confidence interval, the value of z = 1.645.
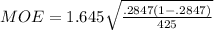
Then, solve.
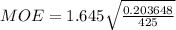
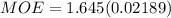
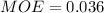
Let's multiply the MOE by 100%.
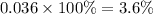
Therefore, about 28.47% ± 3.6% or between 24.87% to 32.07% of the population would be able to successfully reproduce the rhythm.