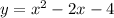Step-by-step explanation
The vertex form of a quadratic function is:
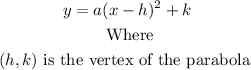
The standard form of a quadratic function is:
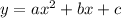
We can do the following steps to solve the exercise.
Step 1: We replace the values of h,k, x, and y into the vertex form of a quadratic equation, and we solve for a.
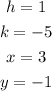
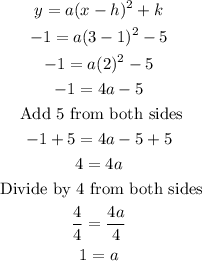
Step 2: We replace the values of a,h, and k into the vertex form of a quadratic equation.
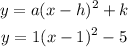
Step 3: We expand the expression inside the parentheses and combine like terms to convert the function into its standard form.
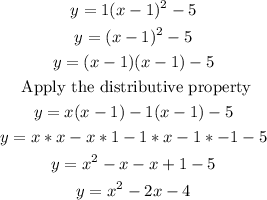
Answer
The equation of the graph in standard form is: