Question

A small yoga studio offers two plans for sessions.•Plan A: Pay a $320 yearly fee and then $5 per session. • Plan B: Pay no yearly fee and $15 per session. Complete each statement. Both plans will cost the same for __?__ sessions. To attend one session each week for a year, plan _?__ will be cheaper.

Answer 1

`\begin{gathered} a)32 \\ b)Plan\: B \end{gathered}`

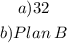
1) Firstly, let's express each plan by using linear equations.

Plan A:

5x+320

Note that the $320 payment is done once, then 5 per session.

Plan B

15x

2) To get to know when opting for plan A or Plan B is not relevant, we need to equate both equations and solve it for x (x stands for the number of sessions)

`\begin{gathered} 5x+320=15x \\ 5x-15x=-320 \\ -10x=-320 \\ 10x=320 \\ (10x)/(10)=(320)/(10) \\ x=32 \end{gathered}`

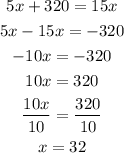
So if you attend 32 sessions then, doesn't really matter which plan is it.

3) Now, let's figure out which plan is more interesting to take:

`\begin{gathered} C_A(x)=5x_{}+320 \\ C(1)=5(1)+320 \\ C(1)=325 \\ --- \\ C_B(x)=15x \\ C_B(1)=15(1) \\ C_B(1)=15 \end{gathered}`

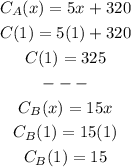
So the plan B is cheaper to attend 1 session