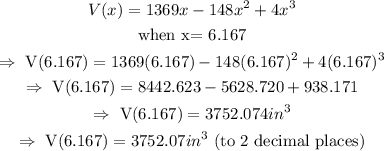The volume of any rectangular box is expressed as:
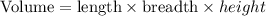
Now, for the box that will be formed from the figure shown in the question, we will have:
length = 37 - 2x
breadth = 37 - 2x
height = x
Thus, we have that:
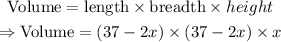
We now simplify the above as:

Now that we have obtained the expression for the volume of the box, we now have to find the value of x that maximizes it.
This is done as follows:
Method
- Differentiate the function V(x) with respect to x, and equate to zero as follows:
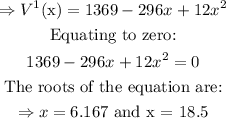
Now we have to find the second derivative of V(x) in order to confirm which value of x makes the function V(x) a maximum
Thus:
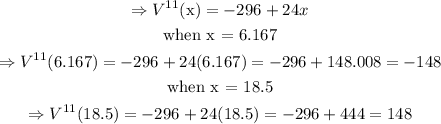
Now since the second derivative is a negative number when x = 6.167, we now know for sure that it is that value of x that maximizes the function V(x), and not x = 18.5.
Thus, we can conclude that the value of x that maximizes the volume of the box is:
x = 6.17 inches (to 2 decimal places)
If we had been asked to find the value of x that minimizes the volume, the answer will have been x = 18.5, because this value of x made the second derivative of V(x) positive.
Now, the maximum volume of the box is obtained by simply substituting the value of x that maximizes the function into the original expression for V(x), as follows: