Question

This Venn diagram shows sports played by 10 students.PLAYSBASKETBALLMaiPLAYSSOCCERMickeyMarcusFranEllalanKarlJadaGabbyJuanLet event A = The student plays basketball.Let event B = The student plays soccer.What is PAB)?O A.A. «0.17B. 1=0.1010

Answer 1

`P(A|B)=(1)/(3)\approx0.333`

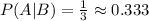
Step-by-step explanation

We want to find the probability P(A|B).

This is a conditional probability and its formula is:

`P(A|B)=(P(A\cap B))/(P(B))`

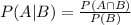
where P(A n B) is the probability that the student plays basketball and soccer and P(B) is the probability that the student plays soccer.

We have that:

`P(A\cap B)=(1)/(10)`

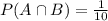
and

`P(B)=(3)/(10)`

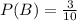
Therefore, we have that:

`\begin{gathered} P(A|B)=(1)/(10)/(3)/(10) \\ P(A|B)=(1)/(10)\cdot(10)/(3) \\ P(A|B)=(1)/(3)\approx0.333 \end{gathered}`

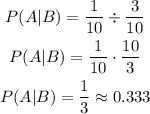
That is the answer.