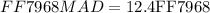Question

4 The number of cars in 5 different parkinglots are listed below.35, 42, 63, 51, 74What is the mean absolute deviation ofthese listed numbers?

Answer 1

The number of cars in 5 different parking lots are given as data points as follows:

`35\text{ , 42 , 63 , 51 , 74}`

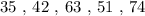
We are to determine the Mean Absolute Deviation ( MAD ). It is a statistical indicator which is used to quantify the variability of data points. We will apply the procedure of determining the ( MAD ) for the given set of data points.

Step 1: Determine the Mean of the data set

We will first determine the mean value of the data points given to us i.e the mean number of cars in a parking lot. The mean is determined by the following formula:

`\mu\text{ = }\sum ^5_(i\mathop=1)(x_i)/(N)`

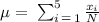
Where,

`\begin{gathered} \mu\colon\text{ Mean} \\ x_i\colon\text{ Number of cars in ith parking lot} \\ N\colon\text{ Total number of parking lots} \end{gathered}`

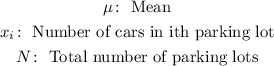
We will use the above formulation to determine the mean value of the data set:

`\begin{gathered} \mu\text{ = }\frac{35\text{ + 42 + 63 + 51 + 74}}{5} \\ \mu\text{ = }(265)/(5) \\ \textcolor{#FF7968}{\mu=}\text{\textcolor{#FF7968}{ 53}} \end{gathered}`

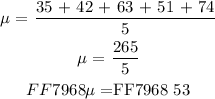
Step 2: Determine the absolute deviation

The term absolute deviation is the difference of each point in the data set from the central tendency ( mean of the data ). We determined the mean in Step 1 for this purpose.

To determine the absolute deviation we will subtract each data point from the mean value calculated above.

`AbsoluteDeviation=|x_i-\mu|`

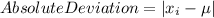
We will apply the above formulation for each data point as follows:

`\begin{gathered} |\text 42 - 53 \\ |\text -2 21\text \\ \textcolor{#FF7968}{18}\text{\textcolor{#FF7968}{ , 11 , 10 , 2 , 21}} \end{gathered}`

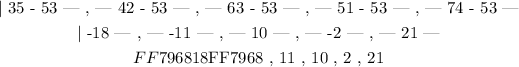
Step 3: Determine the mean of absolute deviation

The final step is determine the mean of absolute deviation of each data point calculated in step 2. Using the same formulation in Step 1 to determine mean we will determine the " Mean Absolute Deviation ( MAD ) " as follows:

`\begin{gathered} \mu_(AD)\text{ = }\frac{18\text{ + 11 + 10 + 2 + 21}}{5} \\ \mu_(AD)\text{ = }(62)/(5) \\ \textcolor{#FF7968}{\mu_(AD)}\text{\textcolor{#FF7968}{ = 12.4}} \end{gathered}`

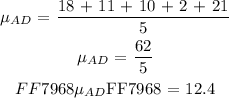
Answer:

`\textcolor{#FF7968}{MAD=12.4}\text{\textcolor{#FF7968}{ }}`