Given:
The points of the triangle:

Required:
To find out if the given triangle is an equilateral triangle or an isosceles triangle or both or none of these.
Step-by-step explanation:
To find if the triangle is an equilateral triangle or an isosceles triangle we will have to first find the length of the sides by distance formula.
Distance formula is given by:
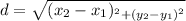
So applying the distance formula on side P₁P₂
Substituting the value of P₁ and P₂ in the distance formula we get
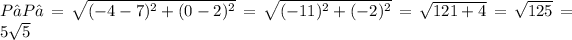
Now lets find the length of P₂P₃
Substituting the value of P₂ and P₃ in the distance formula we get
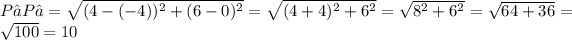
Now lets find the length of P₁P₃
Substituting the value of P₁ and P₃ in the distance formula we get
S now we have the length of all three sides, that is
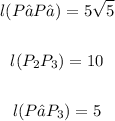
If we add any two sides of triangle then it is greater than the third side so it is a triangle.
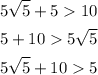
So it is a valid triangle. But the length of all the sides of triangle are different.
In equilateral triangle all the sides are same.
In isosceles triangle any sides are same.
Since here none of the sides are same so it is neither an equilateral triangle nor an isosceles triangle. It is a Scalene triangle with all three sides different.
Final answer:
The answer is none of these.