For the given parallelogram, the diagonals AC and BD intersect at point E. That means;

Substitute for the given values and we'll have;
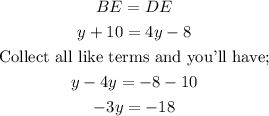
Divide both sides by -3 and you'll have;
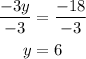
Note that line segment BD is made up of;
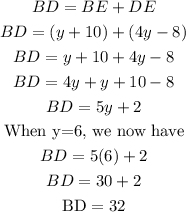
Therefore, the answer is option B