Given: An equation-
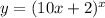
Required: To determine the differentiation of y with respect to x.
Explanation: The differentiation of a logarithmic function is-
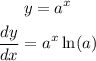
Taking log both sides on the given equation as-
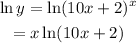
Now, differentiating with respect to x using product rule as-
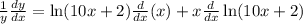
Further simplifying as-
![(dy)/(dx)=y[\ln(10x+2)+(10x)/(10x+2)]](https://img.qammunity.org/2023/formulas/mathematics/college/zt7sxu74qrqwqpulyy68y72lqfvrn8xppn.png)
Substituting the value of y as-
![(dy)/(dx)=(10x+2)^x[\ln(10x+2)+(10x)/(10x+2)]](https://img.qammunity.org/2023/formulas/mathematics/college/mrs6pd300jdlaqyaysrt6yij9cu08lkk0y.png)
Final Answer: Option D is correct.