Given:
The mass of the first sphere is: m1 = 3.699 g.
The mass of the second sphere is: m2 = 3.699 g
The distance between their centers is: d = 3.592 cm
The acceleration of each sphere is: a = 297.727 m/s^2
To find:
Since the spheres are identical in their masses, the force on each sphere is:
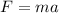
Substitute the values in the above equation and simplify it, we get:
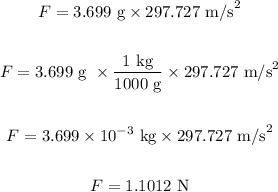
This is the force experienced by each sphere and is has a magnitude equal to the magnitude of the electrostatic force.
The electrostatic force of attraction or repulsion between two charges is given by:
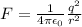
Substitute the values in the above equation and simplify it, we get:

Rearranging the above equation and simplify it, we get:
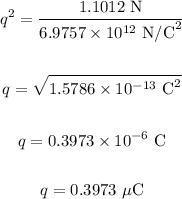
Final answer:
The magnitude of the charge on each sphere is 0.3973 microcolumns.