Question

The scatterplot shows the average number of hours each of 13 people spends at work every week and the average number of hours each of them spends recreational activities every week.Based on the scatterplot,what is the best prediction of the average number of hours a person spends at work every week if that person spends an average of 10 hours on recreational activities every week?A.33 hB.95 hC.50 hD.65 h

Answer 1

We want to find the best prediction of the average number of hours a person spends at work every week if that person spends an average of 10 hours on recreational activities every week.

We will construct a line that adapts to the system by simple linear regression, and then we will find the x-value that makes the line take y=10.

First, we have the data:

We remember that in a simple regression model, we want to write an equation of the form:

`y=\hat{\alpha}+\hat{\beta}x`

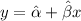
where:

`\begin{gathered} \hat{\alpha}=\bar{y}-\hat{\beta}\bar{x} \\ \hat{\beta}=(nS_(xy)-S_xS_y)/(nS_(xx)-S^2_x)_{} \end{gathered}`

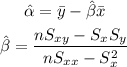
And the Sx, Sy and Sxx are the sums over all the x-values, the y-values and the multiplication of the x-values and y-values (respectively).

We will find those values:

`\begin{gathered} S_x=\sum ^(13)_(i=1)x_i=370 \\ S_y=\sum ^(13)_(i=1)y_i=336.5 \end{gathered}`

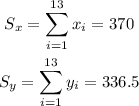
Also, we have:

`\begin{gathered} S_(xx)=\sum ^(13)_(i=1)x^2_i=12600 \\ S_(xy)=\sum ^(13)_(i=1)x_iy_i=8680_{}_{} \end{gathered}`

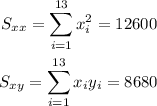
And applying the formula, having in mind that n=13, we get:

`\begin{gathered} \hat{\beta}=(nS_(xy)-S_xS_y)/(nS_(xx)-S^2_x)_{} \\ =(13(8680)-(370)(336.5))/(13(12600)-(370^2)) \\ =(-11665)/(26900) \\ \approx-0.4336 \end{gathered}`

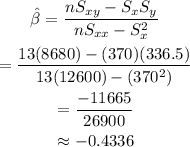
And, for alpha:

`\begin{gathered} \hat{\alpha}=(1)/(n)S_y-\hat{\beta}(1)/(n)S_x \\ =(1)/(13)(336.5)-(-0.4336)(1)/(13)(370) \\ \approx38.2255 \end{gathered}`

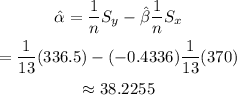
This means that the linear regression equation will be:

`y=38.2255-0.4336x`

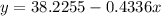
For finding the x-value that will have 10 hours of recreational activities, we replace the 10 value on y, and clear out the variable x:

`10=38.2255-0.4336x`

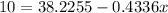
And thus,

`\begin{gathered} 10-38.2255=-0.4336x \\ (-28.2255)/(-0.4336)=x \\ 65.09=x \end{gathered}`

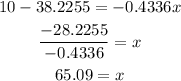
This means that when a person works 65 hours approximately, he will have 10 hours of recreational activities every week.