Given the system of equations. We have:
- For (5,0)
Substitute x = 5 and y = 0 in the equations:
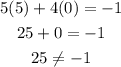
Answer: No
- For (-7, -8)
x = -7 and y = -8
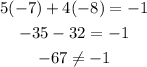
Answer: No
- For (3, -4)
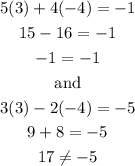
This is satisfied for the first equation but not for the second. Therefore it is not a solution to the system.
Answer: No
- For (-2, -2)
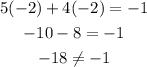
Answer: No