Question

The price of Apple stock, A(X), over a 12 month period decreased and thenincreased according to the equation A(x) = x x 0, where x equals the number ofmonths. The 2 - 6 + 2 price of Baller stock B(x), increased according to theequation B(x) = 3x + 2 over the same 12-month period. When were both stockvalues the same?

Answer 1

The question is: When we're both stock values the same? Then all you have to do is match both equations and solve for x, like this

`\begin{gathered} A(x)=x^2-6x+20 \\ B(x)=3x+2 \\ \text{ Matching you have} \\ x^2-6x+20=3x+2 \\ \text{Subtract 3x from both sides of the equation} \\ x^2-6x+20-3x=3x+2-3x \\ x^2-9x+20=2 \end{gathered}`
`\begin{gathered} \text{Now subtract 2 from both sides of the equation} \\ x^2-9x+20-2=2-2 \\ x^2-9x+18=0 \end{gathered}`

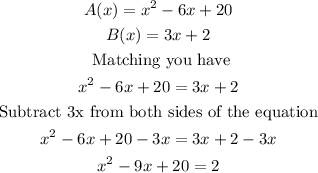
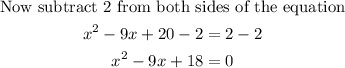
Factoring the trinomial you get

`x^2-9x+18=(x-6)(x-3)=0`

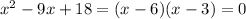
Which implies that

`\begin{gathered} x-6=0 \\ x=6 \\ \text{ or} \\ x-3=0 \\ x=3 \end{gathered}`

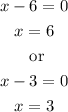
Therefore, since x corresponds to the number of months, then the values ​​of the two shares were equal at 3 and at 6 months.