Question

I have to find the distance form the swings to fountain. help please

Answer 1

The first thing we have to do is locate the points where the swings and the fountain are located on the graph.

`\begin{gathered} Fountain\to(-2,-2) \\ Swings\to(5,-2) \end{gathered}`

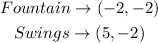
To calculate the distance between the 2 points we use the following equation:

`\begin{gathered} D(F,S)=\sqrt[]{(x_2-x_1)^2-(y_1-y_1)^2} \\ \end{gathered}`

We replace the values of the points F and S:

`\begin{gathered} D(F,S)=\sqrt[]{(5_{}-(-2)_{})^2-(-2_{}-(-2)_{})^2} \\ D(F,S)=\sqrt[]{(5_{}+2_{})^2-(-2_{}+2_{})^2} \\ D(F,S)=\sqrt[]{(7_{})^2-(0_{})^2} \\ D(F,S)=\sqrt[]{(7)^2} \\ D(F,S)=7 \end{gathered}`

So the distance between the swings and the fountains is 7