Question

A medical clinic has a crew of 5, two of which have been infected with a virus althoughthey show no symptoms. If you select two crew members for a task, what is the probability that there is at least one infected person in group assigned for the task.

Answer 1

Answer:

P(at least 1 infected person) = 0.7

Step-by-step explanation:

Note that:

Probability = (Number of possible outcomes) / (Number of total outcomes)

The crew members = 5

Number of infected crew members = 2

Number of uninfected crew members = 3

We want to select two crew members for a task out of 5

Number of total outcomes = 5C2 (Selecting 2 out of 5)

Note that:

`nCr=(n!)/((n-r)!r!)`
`\begin{gathered} 5C2=(5!)/((5-2)!2!) \\ \\ 5C2=(5!)/(3!2!) \\ \\ 5C2=\frac{5*4*\cancel{3!}}{\cancel{3!}*(2*1)} \\ \\ 5C2=(20)/(2) \\ \\ 5C2=10 \end{gathered}`

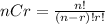
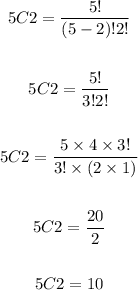
Number of total outcomes = 10

That is, there are 10 ways of selecting 2 crew members from 5

Number of ways of selecting 1 infected person means how we can select two people out of 5 such that 1 one of them will be infected. This means that we will select 1 from the two infected persons, and select the second one from the 3 uninfected persons

Number of ways of selecting 1 infected persons = 2C1 x 3C1

`\begin{gathered} 2C1=(2!)/((2-1)!1!)=(2!)/(1!1!)=(2*1)/(1*1) \\ 2C1=2 \\ \\ 3C1=(3!)/((3-1)!1!)=(3!)/(2!1!)=(3*2*1)/(2*1*1)=(6)/(2) \\ 3C1=3 \end{gathered}`

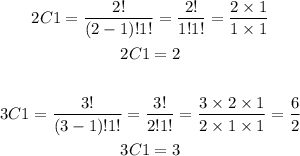
Number of ways of selecting 1 infected persons = 2 x 3

Number of ways of selecting 1 infected persons = 6

Number of ways of selecting 2 infected persons = 2C2

`2C2=(2!)/((2-2)!2!)=(2!)/(2!)=1`

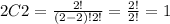
Number of ways of selecting 2 infected persons = 1 way

Probability of selecting 1 infected person = 6/10 = 0.6

Probability of selecting 2 infected person = 1/10 = 0.1

P(at least 1 infected person) = P(1 infected person) + P(2 infected persons)

P(at least 1 infected person) = 0.6 + 0.1

P(at least 1 infected person) = 0.7