Question

Will someone explain to me how I get this done?

Answer 1

The Solution:

The given system of equations are:

`\begin{gathered} x-2y=4\ldots eqn(1) \\ 2x+y=-2\ldots eqn(2) \end{gathered}`

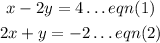
We are asked to solve using the Substitution Method.

Step 1:

From eqn(1), we shall find x in terms of y.

`\begin{gathered} x-2y=4 \\ \text{Adding 2y to both sides, we get} \\ x-2y+2y=4+2y \\ x=4+2y\ldots eqn(3) \end{gathered}`

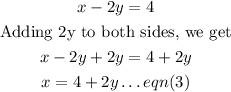
Putting eqn(3) into eqn(2), we get

`\begin{gathered} 2x+y=-2 \\ \text{Putting 4+2y for x, we get} \\ 2(4+2y)+y=-2 \end{gathered}`

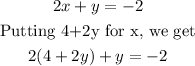
Clearing the brackets, we get

`\begin{gathered} 8+4y+y=-2 \\ \text{Subtracting 8 from both sides, we get} \\ 8-8+4y+y=-2-8 \\ 4y+y=-10 \\ 5y=-10 \end{gathered}`

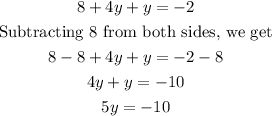
Dividing both sides by 5, we get

`\begin{gathered} (5y)/(5)=(-10)/(5) \\ \\ y=-2 \end{gathered}`

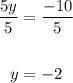
Substituting -2 for y in eqn(3), we have

`\begin{gathered} x=4+2y \\ x=4+2(-2) \\ x=4-4=0 \\ \text{ So, the solution is (0,-2)} \end{gathered}`

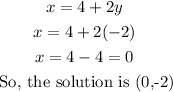
Therefore, the correct answer is x=0, y= -2