hello
to solve this question, we need to draw an illustration
since we are looking for the major arc, we would subtract the minor arc from 360 degrees
major arc YZ =
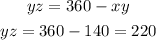
now, we know the angke on the major arc is equal to 220 degrees, we can use this information to solve for the length of the arc.
length of an arc
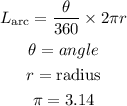
but in this question, we were given the diameter of two segements. we can use that information to solve for the radius
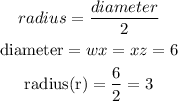
let's insert this and other variables into our equation

from the calculations above, the length of the arc YZ is equal to 11.513