Question

Hi, can you help me answer this question please, thank you!

Answer 1

We are asked to determine the test statistic for two populations. To do that we will use the following formula:

`z=\frac{\bar{x_2}-\bar{x_1}}{\sqrt[]{(SD^2_2)/(n_2)+(SD^2_1)/(n_1)}}`

Where:

`\begin{gathered} \bar{x_1},\bar{x_2}=\text{ population means} \\ SD_1,SD_2=\text{ standard deviations} \\ n_1,n_2=\text{ population sizes} \end{gathered}`

Substituting the values we get:

`z=\frac{83.3_{}-75.4}{\sqrt[]{\frac{(17.8)^2_{}}{19}+\frac{(9.7)^2_{}}{12}}}`

Solving the operations we get:

`z=1.596`

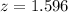
Therefore, the test statistic is 1.596.

To determine the P-value we will determine the probability that the test statistic is less than the value we determined. This is:

`p-\text{value}=P(z<1.596)`

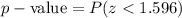
The value of the probability we find it in the z-table using the value z = 1.596, we get:

`p-\text{value}=0.9441`

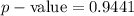
Therefore, the p-value is 0.9441.