Question

A plastic candy container and its dimensions are shown in the figure.What is the closest to the value of the volume?

Answer 1

The volume of this composite figure is the sum of the volume of the cylinder and the cone.

Volume of Cylinder

The formula is

`V=\pi r^2h`

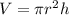
Where

V is the volume

r is the radius

h is the height

Given,

r = 5

h = 17.8

Substituting, we find the volume:

`\begin{gathered} V=\pi r^2h \\ V=\pi(5)^2(17.8) \\ V=1398.01 \end{gathered}`

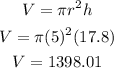
Volume of Cone

The formula is:

`V=(1)/(3)\pi r^2h`

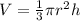
Where

V is the volume

r is the radius

h is the height

Given,

r = 5

h = 6.2

Substituting, we find the volume:

`\begin{gathered} V=(1)/(3)\pi r^2h \\ V=(1)/(3)\pi(5)^2(6.2) \\ V=162.32 \end{gathered}`

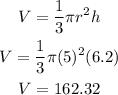
The total volume of the figure is:

1398.01 + 162.32 = 1560.33