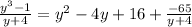Question

Using long division divide y cubed + 0y squared minus 1 by y +4

Answer 1

Answer:
`(y^3-1)/(y+4)=y^2-4y+16+(-65)/(y+4)`

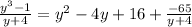
Step-by-step explanation:

Given the expression:

`(y^3+0y^2-1)/(y+4)`

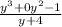
Step 1:

Divide the leading term of the dividend by the leading term of the divisor. Multiply the result by the divisor and subtract the final result from the dividend as follows:

`\begin{gathered} (y^3)/(y)=y^2 \\ \\ \\ y^2(y+4)=y^3+4y^2 \\ \\ \\ (y^3-1)-(y^3+4y^2)=-4y^2-1 \end{gathered}`

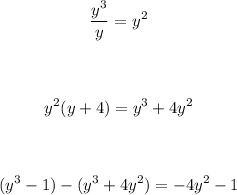
Step 2: Divide the leading term of the obtained remainder by the leading term of the divisor, multiply it by the divisor, and subtract the remainder from the obtained result:

`\begin{gathered} (-4y^2)/(y)=-4y \\ \\ \\ -4y(y+4)=-4y^2-16y \\ \\ \\ (-4y^2-1)-(-4y^2-16y)=16y-1 \end{gathered}`

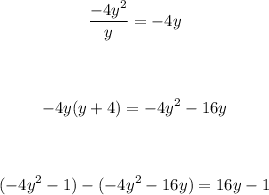
Step 3: Divide the leading term of the obtained remainder by the leading term of the divisor, multiply it by the divisor, and subtract the remainder from the obtained result:

`\begin{gathered} (16y)/(y)=16 \\ \\ \\ 16(y+4)=16y+64 \\ \\ \\ (16y-1)-(16y+64)=-65 \end{gathered}`

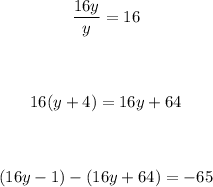
Since the degree of the remainder is less than the degree of the divisor, we would stop.

Therefore, the answer is:

`(y^3-1)/(y+4)=y^2-4y+16+(-65)/(y+4)`