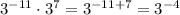Question

I'll send a pic ! I need a rlly fast response !!

Answer 1

The expression given is:

`(3^3\cdot3^(-1))^(-2)`

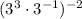
One property of exponents that we know is:

`a^xa^y=a^(x+y)`

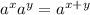
We use this property shown above to simplify the expression:

`\begin{gathered} (3^3\cdot3^(-1))^(-2) \\ =(3^(3-1))^(-2) \\ =(3^2)^(-2) \end{gathered}`

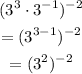
Now, we use the power property of exponents, which is:

`(a^b)^c=a^(bc)`

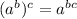
to simplify our expression, fully:

`\begin{gathered} (3^2)^(-2) \\ =3^(2*-2) \\ =3^(-4) \end{gathered}`

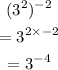
Using the property:

`a^(-n)=(1)/(a^n)`

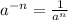
we can write the answer as:

`3^(-4)=(1)/(3^4)=(1)/(81)`

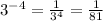
From the choices, given, we can say:

• 2nd choice is correct

,

• 3rd choice is correct

`3^(-11)\cdot3^7=3^(-11+7)=3^(-4)`