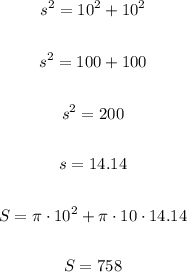Question

Match each solid cone to it’s surface area. Answers are rounded to the nearest square unit

Answer 1

The surface area of a cone is given by the formula below:

`S=\pi r^2+\pi rs`

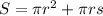
Where r is the base radius and s is the slant height.

So, calculating the surface area of first cone, we have:

`\begin{gathered} s^2=21^2+6^2\\ \\ s^2=441+36\\ \\ s^2=477\\ \\ s=21.84\\ \\ S=\pi\cdot6^2+\pi\cdot6\cdot21.84\\ \\ S=525 \end{gathered}`

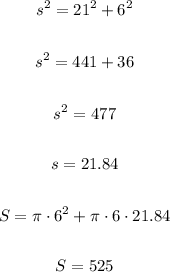
The surface area of the second cone is:

`\begin{gathered} s^2=8^2+12^2\\ \\ s^2=64+144\\ \\ s^2=208\\ \\ s=14.42\\ \\ S=\pi\cdot12^2+\pi\cdot12\cdot14.42\\ \\ S=996 \end{gathered}`

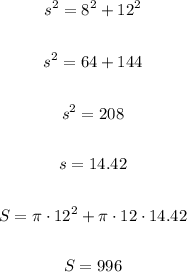
The surface area of the third cone is:

`\begin{gathered} s^2=15^2+8^2\\ \\ s^2=225+64\\ \\ s^2=289\\ \\ s=17\\ \\ S=\pi\cdot8^2+\pi\cdot8\cdot17\\ \\ S=628 \end{gathered}`

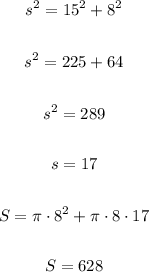
And the surface area of the fourth cone is:

`\begin{gathered} s^2=10^2+10^2\\ \\ s^2=100+100\\ \\ s^2=200\\ \\ s=14.14\\ \\ S=\pi\cdot10^2+\pi\cdot10\cdot14.14\\ \\ S=758 \end{gathered}`