In order to calculate the minimum and maximum usual values, first let's calculate the mean and standard deviation of this distribution:
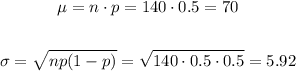
Now, calculating the minimum and maximum usual values, we have:
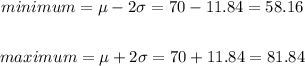
Since the given result is 55, it is an unusual reslt, because it is less tahan the minimum usual value.
Correct option: third one.