Answer:
Volume of the cone is increasing at the rate
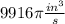 .
.
Explanation:
Given: The radius of a right circular cone is increasing at a rate of
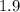 in/s while its height is decreasing at a rate of
in/s while its height is decreasing at a rate of
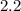 in/s.
in/s.
To find: The rate at which volume of the cone changing when the radius is
 in. and the height is
in. and the height is
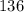 in.
in.
Solution:
We have,
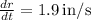 ,
,
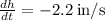 ,
,
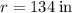 ,
,
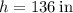
Now, let
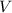 be the volume of the cone.
be the volume of the cone.
So,
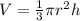
Differentiate with respect to
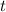 .
.
![(dv)/(dt) =(1)/(3)\pi \left [ r^2(dh)/(dt)+h\left ( 2r \right )(dr)/(dt) \right ]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/wgnhddulqdgmi3xkq2ctms.png)
Now, on substituting the values, we get
![(dv)/(dt) =(1)/(3)\pi\left [ \left ( 134 \right )^2\left ( -2.2 \right )+\left ( 136\right )\left ( 2 \right )\left ( 134 \right )\left ( 1.9 \right ) \right ]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/pm3jqzb40aitsknlewrzts.png)
![(dv)/(dt) =(1)/(3)\pi\left [ -39503.2+69251.2 \right ]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/qpk581o2rt1b9nhloklm6q.png)
![(dv)/(dt) =(1)/(3)\pi\left [ 29748 \right ]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/1l8iayprnjx8yo1qqr6b2a.png)
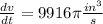
Hence, the volume of the cone is increasing at the rate
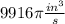 .
.