Question

A circular garden with a radius of 4 ft is planted in the center of a 10 ft square. The part of the square that is NOT the garden is covered with small white rocks. what is the area of the region covered with white rocks?

Answer 1

First, draw a diagram to visualize the situation:

The area of the region covered with small rocks can be found by subtracting the area of the circle from the area of the square.

The area A_s of a square with side L is given by:

`A_s=L^2`

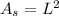
And the area A_c of a circle with radius r is given by:

`A_c=\pi r^2`

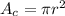
Replace r=4ft and L=10ft into the equations to find the area of the circle and the square:

`\begin{gathered} A_s=(10ft)^2=100ft^2 \\ A_c=\pi(4ft)^2=16\pi ft^2\approx50.265ft^2 \end{gathered}`

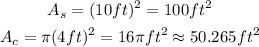
Finally, subtract the area of the circle from the area of the square to find the area of the region covered with rocks:

`A=A_s-A_c=100ft^2-16\pi ft^2\approx49.7ft^2`

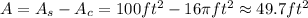
Therefore, the area of the region covered with rocks is exactly 100-16π square feet, which is approximately equal to 49.7 square feet.