Given data:
* The mass of the Moon is,
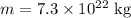
* The radius of the Moon is,
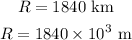
* The height of the Apollo 11 is,
![\begin{gathered} h=122\operatorname{km} \\ h=122*10^3\text{ m} \end{gathered}]()
Solution:
The period of revolution of the Apollo 11 around the Moon is,
![T=2\pi\sqrt[]{((R+h)^3)/(Gm)}](https://img.qammunity.org/2023/formulas/physics/college/rf01milt5ss6701uvdfjk660q826dpau0h.png)
where G is the gravitational constant,
Substituting the known values,
![\begin{gathered} T=2\pi\sqrt[]{((1840*10^3+122*10^3)^3)/(6.67*10^(-11)*7.3*10^(22))} \\ T=2\pi*\sqrt[]{((1962*10^3)^3)/(48.69*10^(11))} \\ T=2\pi*1245.46 \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/h7gjdcvymxwv270ih0kb8vh894576fhigf.png)
Thus, the value of time period is,
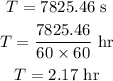
Thus, Apollo 11 takes 2.17 hours to complete orbit once around the Moon.