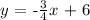Answer:
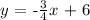
Step-by-step explanation:
Given the y-intercept and a point, we want to get the equation of the line of best fit
We have the slope-intercept form as:
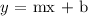
where m is the slope and b is the y-intercept:
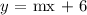
Now, to get m, we substitute the point (4,3)
We substitute 3 for y and 4 for x
We have that as:
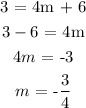
Thus, the equation of the line of best fit is: