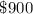Question

The profit P(x) obtained by manufacturing and selling x units of a certain product is given by P(x) = 60x - x2. Determine the number of units that must be produced and sold to maximize the profit. What is the maximum profit?

Answer 1

The number of units that must be produced and sold to maximize the profit is 30 units

`30\text{ units}`

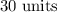
The maximum profit is;

`\text{ \$900}`

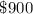
Step-by-step explanation:

Given that the profit P(x) obtained by manufacturing and selling x units of a certain product is given by;

`P(x)=60x-x^2`

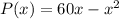
The maximum point is at;

`P^(\prime)(x)=0`

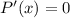
Differentiating P(x);

`\begin{gathered} P^(\prime)(x)=60-2x=0 \\ 60-2x=0 \\ 2x=60 \\ x=(60)/(2) \\ x=30 \end{gathered}`

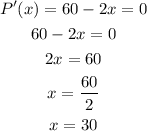
The number of units that must be produced and sold to maximize the profit is 30 units

Substituting x into p(x);

`\begin{gathered} P(30)=60(30)-30^2 \\ P(30)=900 \end{gathered}`

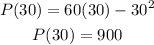
The maximum profit is;

`\text{ \$900}`