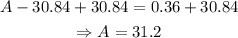Let A be the total amount of money that Mrs. Sorenstam had before buying the school supplies. Let C be the unit price of the compass, M the unit price of the mechanical pencil and R the unit price of the ruler.
The total amount of money required for the school supplies of one student, is C+M+R. Since there are 12 students, the total amount of money required for school supplies is:
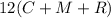
Since Mrs. Sorenstam had a total A of money and she bought the school supplies for 12 students, with 36 cents left after the transaction, then:
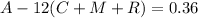
Since C=1.49, M=0.59 and R=0.49, then:
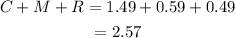
Then, our equation is equivalent to:
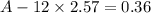
which is the equation that we may write for the first part of the problem.
For the second part, one step is to multiply 12 times 2.57, and then add the result to both sides of the equation to solve for A:
1.- Multiply 12 times 2.57:
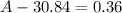
2.- Add 30.84 to both sides of the equation: