Since it is a right triangle, we can use the Pythagorean Theorem. This one states that the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse. In algebraic notation:
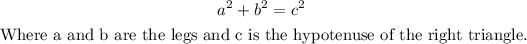
So, in this case, we have:
![\begin{gathered} a=8\operatorname{cm} \\ b=? \\ c=14\operatorname{cm} \end{gathered}]()
![\begin{gathered} a^2+b^2=c^2 \\ (8cm)^2+b^2=(14cm)^2 \\ (8)^2cm^2+b^2=(14)^2cm^2 \\ 64cm^2+b^2=196cm^2 \\ \text{ Subtract }64cm^2\text{ from both sides of the equation} \\ 64cm^2+b^2-64cm^2=196cm^2-64cm^2 \\ b^2=132cm^2 \\ \text{ Apply square root to both sides of the equation} \\ √(b^2)=√(132cm^2) \\ \boldsymbol{b}\approx\boldsymbol{11.49\operatorname{cm}} \end{gathered}]()
Therefore, the measure of the other leg rounded to the nearest hundredth is 11.49 centimeters.