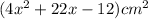Answer:
Explanation:
From the given figure:
• The base of the triangle, b = (4x-2) cm
,
• The perpendicular height, h = (2x+12) cm
The area of a triangle is calculated using the formula:
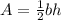
Substitute the given expressions:
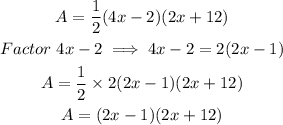
Next, open the brackets:
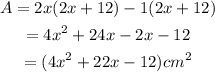
The area of the triangle is: