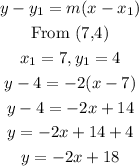Question

Write an equation for the line parallel to g(x)= -2x-6 and passing through the point (7, 4) Write the answer in slop intercept form.

Answer 1

The slope-intercept form is:

`y=mx+c`

So first we will find the gradient:

Parallel lines have the same gradient:

`\begin{gathered} g(x)=-2x-6 \\ \text{The gradient from the equation above is -2} \end{gathered}`

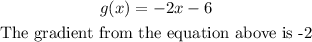
So now that we know the gradient of the line as -2, we will then find the equation of the line using the formula below as it passes through (7,4):

`\begin{gathered} y-y_1=m(x-x_1) \\ \text{From (7,4)} \\ x_1=7,y_1=4 \\ y-4=-2(x-7) \\ y-4=-2x+14 \\ y=-2x+14+4 \\ y=-2x+18 \end{gathered}`