The given number is

This number is a repeating decimal number, which is a rational number because it has a pattern that repeats infinitely. That pattern or period is 2.
To transform this decimal number into a fraction, we need to do it as follows

Notice that the difference is form by the complete number without a decimal point (62), and the digits before the repeating decimal (6). The denominator is formed by nines and zeros, in this case, we use one 9 because there's only one repeating digit, we use one 0 because there's only one digit between the decimal points and the repeating digit.
Now, we solve the fraction and simplify
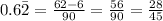
Therefore, the fraction 28/45 is the one that represents the repeating decimal 0.6222...