AB = 3x + 4
BC = 7x + 9
AB + BC = AC
AC = 143
Let us add AB and BC then equate their sum by 143
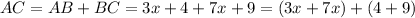
First, step add the like terms
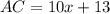
Equate AC by its length 143
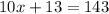
Now we have an equation to solve it
To solve the equation let us move 13 from the left side to the right side by subtracting 13 from both sides
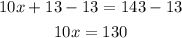
To find x divide both sides by 10 to move 10 from the left side to the right side
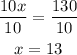
Now let us find AB and BC
Substitute x by 13 in each expression
AB = 3(13) + 4 = 39 + 4 = 43
BC = 7(13) + 9 = 91 + 9 = 100
The length of AB is 43 units
The length of BC is 100 units