D)
To find the probability of selling 25 cheesecakes:
It is impossible to find the probability of selling 25 cheesecakes.
So,
P(x=25)=0
The probability of selling 25 cheesecakes is 0.
E)
To find the probability of selling at most 10 cheesecakes:
That is,
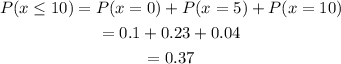
Therefore, the probability of selling at most 10 cheesecakes is 0.37.
F)
To find the expected number of cheesecakes sold on any given day using the discrete probability distribution:
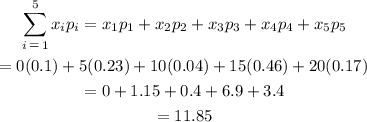
Hence, the expected number of cheesecakes sold on any given day using the discrete probability distribution is 11.85.